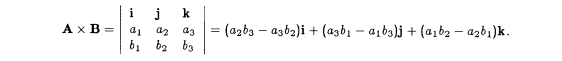Calc 1
Teaches problem-solving skills to find limits, differentiation, and integration. Concept of limits, derivatives, type of functions, use differentiation rules, integrals, applications of differentiation, antidifferentiation, and applications of integration.
Example
Suppose a vehicle travels according to the rule f (t) = 3t^3 -t. Find its velocity at time t = 4. Even though you have in mind a special time t = 4, you cannot substitute t = 4 until the end. (You don’t want f (t) = 44. A constant function has velocity zero! What you will use is f (4) = 44.) First, find the average velocity using dt or h:
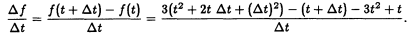
3t^2 cancels with -3t^2 and also t cancels -t. This produces
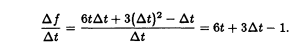
The division removed dt from the denominator. Now let dt go to 0. The limit is f’(t) = 6t -1 = v(t). At t = 4, the velocity is v(4) = 6 x 4 -1 = 23. To find acceleration, go back to the formula for velocity (before you plugged in t = 4). Take the derivative of v(t) = 6t – 1:
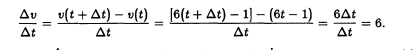
Calc 2
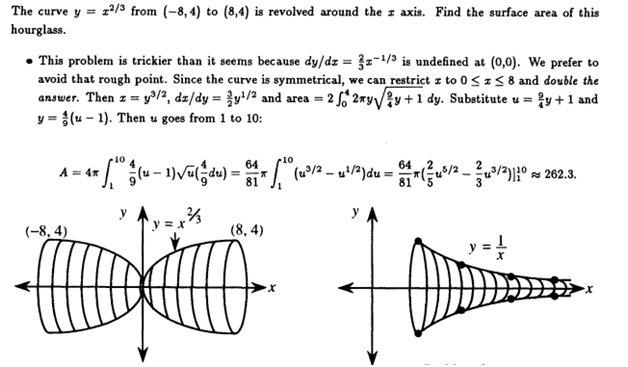
Continues the study of the calculus of algebraic and transcendental functions, graphing such as Polar, rectangular, and parametric, power series, indefinite and definite integrals, and methods of integration. Methods of integration are used by determining the volume, work, arc length, and area. Some of these methods are used by Shell’s, Dish-washer, and cross-section.
Calculus 3
This course focuses on many of the concepts of function limit continuity, derivative integral, Vector from the 3D spaceplane. This course is the introduction of vector functions, multivariate functions, partial derivatives, and multiple integrals.
Cross product